1. Einführung
2. Gravitation, Entropiekraft und Raumzeit
3. Entropiekonstante des kosmischen Universums
4. Dunkle Energie und Dunkle Materie
5. Beschleunigte Expansion des Universums
6. Grenzwerte im Mikrokosmos
7. Betrachtungen im übergreifenden Universum
8. Entropiekraft und Dunkle Materie in kosmischen Systemen
9. Quantenphysikalische Gravitations-, Entropie- und Energiefelder
10. Bosonen, Fermionen und das Gravitationsentropiefeld
11. Massen, Ladungen und Energien von Elementarteilchen
12. Quantenmechanische Vermittlung der vier Fundamentalkräfte
13. Entropiefeld und Kosmologisches Standardmodell
14. PDF Download / Tabellen A und B
4. Dunkle Energie und Dunkle Materie
Nach eingehender heuristischer Betrachtungsweise eines sich in der Zeitdimension kugelförmig ausdehnenden Raumes setzt sich die Entropiekonstante unseres Universums wie folgt zusammen:
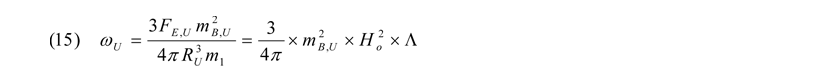
Λ ist dabei der Term, welcher der Kosmologischen Konstante entspricht, die Einstein in sein Kosmologisches Modell der ART eingeführt hat. Setzen wir Gleichung (12) in Gleichung (15) ein, lösen auf und stellen nach Λ um, erhalten wir:

Nach den aus der Einsteinschen ART zu berechnenden Gleichungen kann man mit Hilfe der Kosmologischen Konstanten direkt auf den Anteil der Dunklen Energie im Universum schließen. Der anhand der Entropiekonstante (mittels der neu eingeführten Entropiekraft) errechnete Wert der Kosmologischen Konstante müsste also über die Gleichung der ART (17) zu einem Wert der Dunklen Energie von 73 ± 3 % führen, wie die Auswertungen der WMAP-Mission letztendlich ergeben haben:

Wie man erkennt, hat nach dieser Berechnung über die Entropiekonstante der Anteil der Dunklen Energie einen Faktor von 0,69813. Dies bestätigt den aus dem WMAP-Experiment ermittelten Wert für die Dunkle Energiedichte von 0,73 ± 0,03 in erster Näherung ziemlich gut. Auch über eine ganz und gar nicht heuristische Berechnungsgrundlage sollte man exakt auf den oben berechneten Wert der Dunklen Energie bezogen zur Kritischen Energiedichte EDkrit kommen. Über die Formulierung (10) gelangt man zu einer kritischen Energiedichte EDART und über die umgestellte und integrierte Formel (5) zu einer entropisch bedingten Energiedichte EDEntr am Gleichgewichts- bzw. Hubbleradius folgender absoluter Größen, welche sich, wie es sein muss, um den Faktor 4 unterscheiden, wenn man wieder Postulat 2 zum Ansatz bringt:
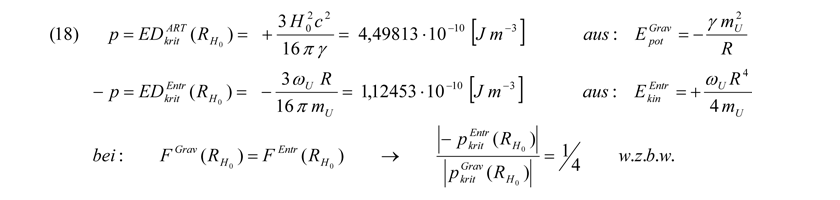
Die WMAP-Mission hat eindeutig festgestellt, dass sich unser Universum bezogen auf die kritische Dichte messbar zu nur ca. 4,4 % Energiedichte aus baryonischer Masse (BM) zusammensetzt. In Bezug auf das Postulat 2 bedeutet dies nichts anderes, als dass unser Universum gegenüber dem Hubble-Radius RHo radial um knapp das Dreifache größer sein müsste. Ignoriert man allerdings den Fakt der seit den 1990-iger Jahren ins Spiel gebrachten beschleunigten Expansion des Universums, lässt dies vorerst einmal zwei sich widersprechende Interpretationen zu:
a) Das Universum ist gemäß konservativem kosmologischem Standardmodell glatt bzw. nur verschwindend offen mit einem Krümmungsfaktor von k ≈ 0. Dann fehlen Energiedichtenbeträge von ca. 96 %, welche man zusammen als Dunkle Energie und Dunkle Materie bezeichnet.
b) Das Universum ist hyperbolisch, also real offen, mit einer Krümmung von k = –1. Diese Behauptung hätte zur Konsequenz, dass der Abbremseffekt der Gravitation durch einen im Universum verteilten gleichmäßigen negativen Druck kompensiert werden müsste, welchen man auch als antigravitative Komponente (Wiedergeburt der Einsteinschen Kosmologischen Konstante Λ) interpretiert.
Unsere Theorie auf die Hypothese a) angewandt bedeutet, dass wir wider besseren Wissens unterstellen müssten, der Druck aus Entropischer Energie wäre positiv, also gravitativ unterstützend, wie gefordert. Um, wie über die Formeln (16), (17) und (18) auf einen Anteil an Dunkler Energie bezogen zur Kritische Dichte der ART von ΩΛ = 0,69813 zu kommen, muss der Radius des Universums RU gegenüber dem Hubble-Radius um Ʀ größer sein, während die entropische Energiedichte den geforderten Wert ΩΛ annehmen sollte. Gleichzeitig darf dabei der sich ergebende Wert für die baryonische Energiedichte ΩBM nicht von dem der WMAP-Mission abweichen, damit die Konsistenz unserer Theorie mit den experimentellen Daten gewahrt bleibt,
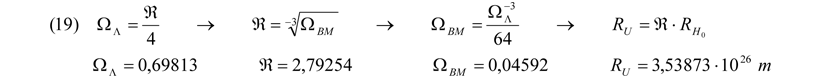
was, wie aus (19) ersichtlich, durchaus der Fall ist. Doch wo bleiben die restlichen ΩDM ≈ 0,25 zur kritischen Energiedichte wie bei a) gefordert, genau jene, welche man der Dunklen Materie DM zuschreibt? Müsste sich über (19) eigentlich nicht eine kumulative Energiedichte aus ΩΛ und ΩDM von ΩDM+Λ ≈ 0,95 ergeben? Diese errechnet sich auch, da ja nach unserer Theorie, wenn man (18) richtig unter die Lupe nimmt, vom Anteil der Kritischen Dichte der ART Ωkrit = 1 ein Anteil an Entropischer Dichte von ΩEntr = 0,25 abgezogen werden sollte, sodass die wirkliche Kritische Dichte, auf welche man sich beziehen muss, Ωkrit,real = 0,75 beträgt. Folgende neue Werte errechnen sich nun:
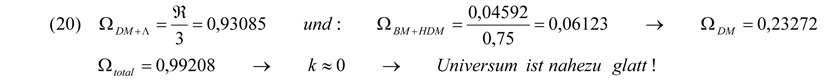
Dabei ergeben sich folgende allgemeine formale Zusammenhänge:
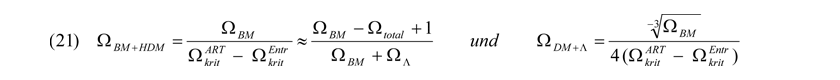
Zu den ca. 4,6 % Anteil an experimentell messbarer baryonischer Materie BM (davon etwa gerade mal ein Zehntel leuchtende Sterne: der überwiegende Teil freier Wasserstoff, gefolgt von Helium und schwereren Elementen) unseres Universums gesellen sich also laut Theorie ungefähr 1,5 % an so genannter Heißer Dunkler Materie HDM (Schwarze Löcher, Neutrinos und möglicherweise unentdeckte Elementarteilchen).
Zieht man von den nun realen ca. 93,1 % „Dunklen Energiequellen“, gespeist aus entropischer Energie, den hypothetischen 69,8 %-igen Anteil an Dunkler Energie ab, so hat man einen Wert des Dunklen-Materie-Anteils von ungefähr 23,3 %.
Das Universum ist demnach leicht geöffnet. Verglichen also mit den obigen Werten approximieren unsere Berechnungen durchaus mit dem Lambda-CDM-Modell recht gut.
Ist dem letztendlich wirklich so? Keinesfalls, denn die entropischen Energiedichten implizieren ja negative antigravitative Drücke und überkompensieren so die abbremsende Wirkung der Materie im Universum ganz erheblich, was noch weit über die Hypothese b) herausgehen würde. Wir werden demzufolge gleich sehen, dass unser Universum deshalb nicht nur wie in einem quasi leeren Raum, sondern wie in einem Raum, welcher mit immer weiter steigender Sogwirkung bzw. negativer Drücken ausgestattet ist, expandiert.
>>> zum nächsten Kapitel (Beschleunigte Expansion des Universums) >>>
