1. Einführung
2. Gravitation, Entropiekraft und Raumzeit
3. Entropiekonstante des kosmischen Universums
4. Dunkle Energie und Dunkle Materie
5. Beschleunigte Expansion des Universums
6. Grenzwerte im Mikrokosmos
7. Betrachtungen im übergreifenden Universum
8. Entropiekraft und Dunkle Materie in kosmischen Systemen
9. Quantenphysikalische Gravitations-, Entropie- und Energiefelder
10. Bosonen, Fermionen und das Gravitationsentropiefeld
11. Massen, Ladungen und Energien von Elementarteilchen
12. Quantenmechanische Vermittlung der vier Fundamentalkräfte
13. Entropiefeld und Kosmologisches Standardmodell
14. PDF Download / Tabellen A und B
10. Bosonen, Fermionen und das Gravitationsentropiefeld
Die hypothetisch elementarsten Teilchen, angenommen Wechselwirkungen mit den oben beschriebenen Feldern würden nicht existieren, sollten Objekte mit den Planck-Abmaßen RPlanck von ca. 1,62·10-35 m (entsprechend einem Volumen von ungefähr 1,8·10-104 m3) nach Gleichung (26) sein, welche sich völlig isotrop und ausfüllend durch alle Richtungen des Raumes bewegen. Dabei gelten dann in der Raumzeit Werte für dieses hypothetische Elementarteilchen mit einem Impulsspektrum I von Null (eigentlich von etwa 10-62 Nsm-1) bis zu einer Größe gemäß Gleichung (69) von ħ/Rplanck (ca. 6,5 Nsm-1). Wir multiplizieren nun den Geschwindigkeitsterm pro forma im Zähler und Nenner mit der Lichtgeschwindigkeit:
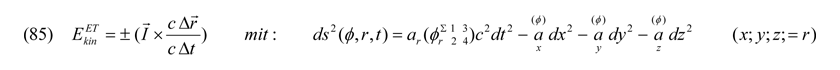
Die Betrachtung des Zeittermes c2dt2 des invarianten Raumzeitparameters ds2 bedeutet, dass jedes Teilchen bezogen auf alle Inertialsysteme sämtliche Bewegung sowohl vorwärts als auch rückwärts durch die Zeit nimmt. Und da nun in einer integral glatten Raumzeit kein Raummaß im „Teilchen-Universum“ gegenüber einem anderen bzw. kein o.g. Teilchen in Bezug zu einem anderen im „Raum-Universum“ irgendwie unterscheidbar ist, hat eine Summe von ds2 = 0 mit a = 1 zur Konsequenz, dass gemäß der Symmetriebetrachtung der Speziellen Relativitätstheorie (SRT) alle dadurch gekennzeichneten Ereignisse auf der Lichtkugel stattfinden, also lichtartig sein müssen. Die elementaren supersymmetrischen Bosonen laufen demzufolge mit Lichtgeschwindigkeit und damit vollkommen ruhemasselos durch den Raum, weil
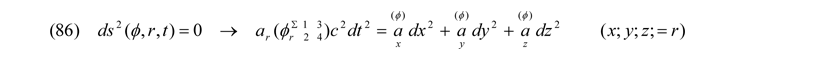
und damit
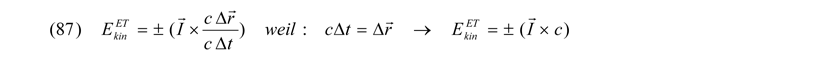
ist. Pro Teilchen treten also immer gleiche positive und negative Beträge auf. Energie und Impuls sind äquivalent. Das hypothetische Teilchen ist somit sein eigenes Antiteilchen und damit solange ein masse-, spin- und ladungsfreies supersymmetrisches Boson, solange keine Wechselwirkungen mit einem der oben beschriebenen Potentialfelder erfolgt. Unter dem so unproblematisch zu interpretierenden Energieerhaltungssatz kann damit jedes Boson gemäß des skalaren Vektorproduktes ± (I x c) auf Grund des Fluktuationspotentials innerhalb seiner Planck-Länge jeden beliebigen positiven und negativen gleichen Wert bis hin zur Planck-Energie annehmen. Dabei ist es aus symmetrischen Gründen immer möglich, dass ein so produziertes Boson im Weiteren als lokal getrenntes Teilchen-/Antiteilchenpaar über beliebige Entfernungen gemäß (87) verschmiert (superponiert, verschränkt) ist.
Durchlaufen die o.g. supersymmetrisch verschränkten Bosonenpaare statische Energiefelder bestimmter Längenskalen, können diese unter Umständen je nach Art der in den Potentialtöpfen herrschenden Kraftkomponenten und Schwingungsmoden durch Interaktion dann nur noch ganz bestimmte skalare Energie- bzw. Massezustände aus vektoriellen und skalaren Werten, wie Impuls, Spin, Kraft, Beschleunigung, Geschwindigkeit, Ladung und Farbe, durch herrschende Symmetriebrüche bzw. Krümmungen der Raumzeit, annehmen. Allgemein gilt nämlich sowohl für kausale (und nichtkausale) Beschreibungen das reale (imaginäre) Raum-Zeit-Abstandsmaß:
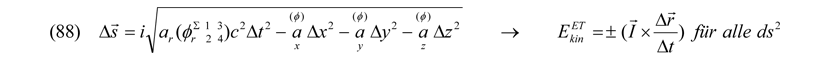
Die Einsteinsche Relativitätstheorie sollte also jetzt beim Wechselwirken der supersymmetrischen Bosonen mit mehr oder weniger symmetrischen bzw. gekrümmten oben beschriebenen Potentialfeldern folgende drei Interpretationen zulassen:

Die Wechselwirkungen lösen innerhalb der Potentialtöpfe charakteristische interferenzfähige Störungen in den stehenden Wellenmustern aus, welche sich dann aufgrund von Tunneleffekten über die Potentialgrenzen hinweg mit bis zu Lichtgeschwindigkeit theoretisch über das ganze Universum ausbreiten (als Ortsfunktionen der nun dynamischen Wahrscheinlichkeitswellen IψI2). Dabei ist der Impuls m0v des induzierten Teilchens nach Gleichung (90) mit den Impuls der mit ihm jetzt assoziierten Welle E/c identisch und austauschbar (siehe De-Broglie-Gleichung weiter unten). Diese Assoziierung eines auch unter Umständen verschränkten Welle-/ Teilchenpaares (Spin+/-; Materie+/-) wird instantan dann aufgehoben, wenn das System durch bestimmte äußere Impulse beeinflusst wird. Eine nämlich dadurch realisierte stärkere Lokalisierung erzeugt dabei simultan in der ganzen Welle ein gewisses zusätzliches und chaotisches Energiespektrum, welches ausreichend ist, dass die Welle ihre Interferenzfähigkeit auf Anhieb verliert. Die Wahrscheinlichkeitswelle des mit der Welle assoziierten Elementarteilchens bricht deswegen an der Stelle der Lokalisierung unter Implizierung des mit ihm eigentlich superponierten Teilchens in Befolgung der Gleichung (91) sofort in sich zusammen. Die dynamische Wahrscheinlichkeitswelle ist somit als eine Beeinflussung statischer Wellen durch elementare interagierenden Teilchen zu interpretieren, wobei die ausgelöste interferenzfähige Störung (Wahrscheinlichkeitswelle des mit der Welle superponierten Teilchens) nur solange aufrecht erhalten werden kann, solange sich die Teilchen-Welle relativ unabhängig von äußeren Einwirkungen durch die Raumzeit gemäß (89) und (90) bewegt.
Die eigentlichen Störungen (dynamische Wahrscheinlichkeitswellen über die gesamte universelle Raumzeit) der statischen Potentialfelder sollten auch folgendermaßen zu verstehen sein:
Vom Standpunkt eines sich in Bezug zum Potentialfeld (frei fallenden) bewegenden Teilchens schwingen die eigentlich stehenden Wellenmuster der Potentialfelder mit dem Ortsmaß Rλ,Feld mit einer umso höheren Frequenz ʋFeld, je schneller sich das Teilchen mit einer bestimmten Geschwindigkeit vT bewegt. Da in allen Inertialsystemen nur die Lichtgeschwindigkeit konstant ist und wenn man nun die betreffenden Teilchengeschwindigkeiten über die Feldfrequenz mit der Lichtgeschwindigkeit koppelt, ergeben sich resultierenden Wellenlängen für bewegte Teilchen λT in allen Inertialsystemen Is zu:
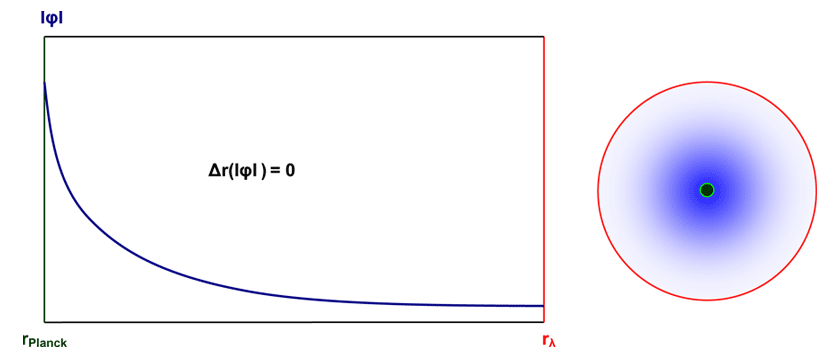
Ruht das Teilchen ist seine Frequenz gleich Null. Bis zum Grenzfall vT = c erhöht sich folglich dessen Frequenz bzw. erniedrigt sich seine Wellenlänge. Bewegt sich das Teilchen exakt mit Lichtgeschwindigkeit, entspricht dessen Wellenlänge genau dem des dazugehörigen Potentialtopfmaßes RλFeld. Da in der Quantentheorie Längenskalen und damit Wellenlängen immer umgekehrt proportional zur Energie eines Systems sind, ergibt sich hier ein Widerspruch, da wir ja explizit auch Teilchen mit Ruhemassen m0 betrachten wollen, welche aber in (92) nicht berücksichtigt wurden. Deshalb führen wir diese einfach sowohl im Zähler als auch im Nenner obiger Gleichung ein:
Nun ist aber das Produkt aus Potentialtopfmaß und der dazugehörigen Ruhemasse des Teilchens ganz eindeutig mit dessen konstanter quadratischer Gesamtladung Q2 zu identifizieren, welche nach Konvention die oben gezeigte Größe hat und der so genannten Planck-Ladung entspricht. Wir bekommen so in den Zähler das Plancksche Wirkungsquantum ħ und in den Nenner den Impuls m0v und damit die De-Broglie-Gleichung. Im direkten Umkehrschluss kann man auch sagen, dass der Impuls des sich bewegenden Teilchens invers proportional zur Wellenlänge seiner erzeugten dynamischen Wahrscheinlichkeitswelle ist.
Bewegte Teilchen induzieren demzufolge aus ihrer „ruhenden Sicht“ Störwellen im ansonsten statischen Wellenmuster der dazugehörigen Potentialfelder, deren Wellenlängen wie beschrieben von ihrem Impuls abhängen. Bei ruhemassebehafteten Teilchen, die sich bewegen, verschwindet wie in Gleichung (93) zu sehen die Planck-Ladung vollständig zugunsten einer Welle. Das heißt, dass bei Teilchen mit einer elektrischen Ladung (als Teil der Planck-Ladung), sobald sich diese bewegen, ihr eigenes elektrisches Feld einer dementsprechenden (magnetischen) Welle weicht.
Aus der „ruhenden Sicht“ der Störwellen wiederum (welche ja nichts anderes als stehende statische Wellenmuster eines Potentialfeldes sind) zeigen sich bewegte Teilchen mit Planck-Ladung. Das bedeutet unter anderem eben auch nichts weiter, als dass der Magnetismus, also ein dementsprechendes spezielles Wellenmuster-Potentialfeld, (elektrische) Felder im sich bewegenden Teilchen induziert.
Über die Einbeziehung von Aspekten der Speziellen Relativitätstheorie (SRT) gelangt man so zu einer simplen Erklärung des Wellen-Teilchen-Dualismus für reale Inertialsysteme: Für das Teilchen gibt es nur sich bewegende Wellen oder es gibt eben kein Teilchen (wenn die Länge der Welle Null ist). Und für die Welle gibt es nur sich bewegende Teilchen oder es gibt eben keine Welle (wenn der Impuls des Teilchens Null ist). Falls man also in der Physik Unendlichkeiten, wie zum Beispiel auch bei der relativistischen Masse-/ Energiebetrachtung angewandt, nicht zulässt bzw. als nicht existente Zustände deklariert, muss man feststellen, dass das Eine (Teilchen) ohne das Andere (Welle) definitiv nicht existieren kann. Und genau diese wechselseitige Abhängigkeit führt zu der engen Verflechtung, zur untrennbaren Symbiose von Welle und Teilchen. Zur Dynamik von Elektrizität und Magnetismus. Zu den Elektromagnetischen Welleneigenschaften, die schon Maxwell mit seinen berühmten Gesetzen und im Vorgriff der SRT (da er sie noch nicht kennen konnte) so exakt beschrieben hat.
Jedoch gibt es hier eine Einschränkung, da es Realität ist, dass die Wellenfunktion bei bestimmter äußerer Einflussnahme instantan unter Hervorbringung des alleinigen Teilchens, in sich zusammenbricht. Das könnte so interpretiert werden: Die Wellenfunktion eines (frei fallenden) und sich deshalb mit konstanter Geschwindigkeit und konstantem Vektor bewegenden Teilchens ist gekennzeichnet durch ebenfalls eine zeitlich und räumlich konstante und damit interferenzfähige Wellenlänge. Wirkt eine bestimmte Beschleunigung dieser Konstanz im Vektorimpuls entgegen, werden instantan die Zustände echter (frei fallender) Inertialsysteme gebrochen, so dass nun (zusätzlich zu einer möglichen Interferenzunfähigkeit des Systems wegen jetzt raumzeitlich inkonstanter Wellenlängen) das „Inertialsystem Teilchen“ und das „Inertialsystem Potentialfeld“ gemäß SRT (Gleichung 91) keine gemeinsamen konsistenten Schlussfolgerungen mehr übereinander realisieren können. Das heißt: Wirkt etwas von außen beschleunigend auf ein sich bewegendes Teilchen ein, indem man es z. B. fixiert, maskiert, detektiert usw., verschwindet unter bestimmten Umständen und Wahrscheinlichkeiten dessen Anteil der bis dato mit ihm superponierten Welle mit dem Ergebnis, dass man nun ein (elektrisch geladenes) Teilchen hat, welches sich allein nach den Gesetzen der klassischen Physik weiterbewegt.
Doch jetzt zu der Frage, wie welche Potentialfelder welche Elementarteilchen generieren:
In Auswertung des mikroskopischen Massenspektrums ergeben sich über die Gleichungen (82) (siehe auch Tabelle B) Einteilungen in folgende fünf Kategorien. Die Energien in stark gekrümmten Raumzeitpotentialen (relativistische Grenzen EER) sind dabei bezogen auf die Achse(n) in Richtung der Potentialtopflängen Rλ (entsprechend der Comton-Wellenlänge):
a) rein gravitative Potentiale mit Unterschreitung von RGG (Gleichung 83) von EPlanck (≈ 1,2·1019 GeV) bis etwa 505 GeV
b) abnehmende gravitative und zunehmende entropische Potentiale mit Unterschreitung von RER (Gleichung 84) bis ca. 1,7 MeV
c) zunehmende entropische und abnehmende gravitative Potentiale mit Überschreitung von RER bis ungefähr 0,7 eV
d) entropisch dominierte Potentiale mit großer Überschreitung von RER bis etwa 10-34 eV
e) rein entropische Potentiale weit außerhalb von RER von ca. 10-34 eV bis EPlanck
Dabei ergeben sich innerhalb der Kategorien folgende Abhängigkeiten von Symmetrieeigenschaften (z. B.: +6/S++Planck, ER), Potentialbeträge IφΣI, der Potentialtopfmaße Rλ, des Gleichgewichtsmaßes RGG und der relativistischen Entropiegrenze RER mit den experimentellen und hypothetischen Zuordnungen der durch Wechselwirkungen mit den Feldern entstehenden Teilchen des Standardmodells*:
a) (**2-/*2-) = ‒6/S++λ I-φ1I = I-φ2I > I-φ3I = I-φ4I / RER > RGG > Rλ supersymmetrische Bosonen
b) (***2-/*1-/**1+) = ‒3/ŝ++GG I-φ1I = I-φ2I > +φ3 > I-φ4I / RER > Rλ > RGG t*, H, Z0*, W±*, b*, τ*, c*, μ*, s*, ϑτ* d*, u*, 8 Gluonen*
c) (**1-/*1-/***2+) = +2/ŝ+GG, ER +φ2 = +φ3 > I-φ1I > I-φ4I / Rλ > RER > RGG e*, ϑμ*
d) (**1-/***2+/*1+) = +4/ŝ++GG, ER +φ2 = +φ3 > I-φ1I > +φ4 / Rλ > RER > RGG ϑe*, b) – d): virtuelle Photonen*
e) (**2+/*2+) = +6/S++Planck, ER +φ2 = +φ3 > +φ1 = +φ4 / Rλ > RER > RPlanck: Photonen*, ab ca. 505 GeV bis EPlanck: Gravitonen
Durch diese heuristische Betrachtung ergeben sich folgende nachvollziehbare Interpretationen:
Die am symmetrischsten Energiebereiche der Kategorie a) von ca. 505 GeV bis ungefähr 1019 GeV sowie der Kategorie e) von etwa 10-34 eV bis wiederum etwa 1019 GeV stellen Felder für ruhemasselose absolut stabile o.g. Teilchen (tZerfall = ∞) dar, welche Störungen (Wellenfunktionen) in den betreffenden Energiefeldern auslösen und sich nun mit jenen assoziiert (in Superposition) mittels Lichtgeschwindigkeit ausbreiten. Resultierende Photonen mit Spin 1 aus e) beanspruchen dabei einen Energiebereich von 10-34 eV bis 505 GeV und decken damit sämtliche elektromagnetischen Wellenlängen- sowie Gamma-Spektren aller elementaren und hadronischen Teilchen des Standardmodells ab. Hinsichtlich energetischer Erwägungen heraus sollten somit sämtliche Photonen aus Kategorie e) als völlig identisch mit den in den Feldern der Kategorien b) bis d) emittierten Photonen zu identifizieren sein. Ebenso dürfte auch ein Zusammenhang zwischen den virtuellen Gravitonen bzw. symmetrischen Bosonen der Kategorie a) mit Spin 0 bzw. 1 und den Teilchen (Gravitonen) der Kategorie e) zu ziehen sein, welcher im Ergebnis zu einer interpretierbaren quantenmechanischen Wechselwirkung der Gravitation mit Spin 2 führen könnte.
Mit kleiner werdenden gravitativen bzw. größer werdenden entropischen Potentialen in den Kategorien b), c) und d) werden alle Teilchen mit Spin 0, 1 und (2n+1)/2 des Standardmodells generiert. Ihre Massen bzw. Energien sinken dabei von b) bis d) stetig ab. Unter bestimmten Umständen werden an den jeweiligen Potentialtopfmaßen gemäß Gleichung 69 im übertragenen Sinne virtuelle Bosonen (Z0, W±: Schwache Kraft), Gluonen (Starke Kraft) sowie virtuelle Photonen (Elektromagnetische Kraft) ausgetauscht.
Mathematisch können die oben gemachten Aussagen folgendermaßen gestützt werden:
Abbildung 12: Potentialgradientenbeträge in den Potentialtöpfen der Kategorie a)
Da hier alle vier Potentiale φΣ völlig symmetrisch verteilt (negative Potentiale) sind, müssen wiederum alle Raumzeitabstandsmaße ds2λ zwischen den Feldern und den agierenden elementaren Bosonen (Teilchen) gleich Null sein.
Damit präsentiert sich im unscharfen Potentialtopf der Kategorie a) nach Gleichung (89) ein ruhemasseloses Teilchen, welches sich in der Zeit sowohl vor als auch zurückbewegt bzw. anders ausgedrückt zwischen gleichen positiven und negativen Energiebeträgen oszilliert. Dies wiederum geht mit einer Störung der statischen Wellenfunktion und Auslösung einer dynamischen Welle (die Energie der betreffenden Wellen sind größer als 505 GeV!) einher. So resultiert aus diesem Prozess ein sich mit Lichtgeschwindigkeit bewegendes Teilchen, assoziiert mit einer dynamischen sich im Raum ausbreitenden Welle.
Abbildung 13: Potentialgradientenbeträge in den Potentialtöpfen der Kategorie b)
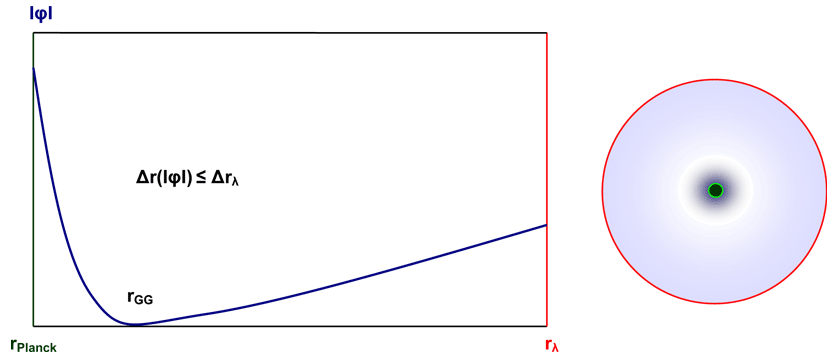
Wenn nun die Raumabstandsmaße dr2λ über alle drei Dimensionen integriert wegen der gleichzeitigen Anwesenheit der Potentiale φGrav und φEntr in der nun asymmetrisch gekrümmten Raumzeit (positive und negative Potentialanteile) bezüglich der Zeitkomponente c2dt2λ kleiner werden, muss ds2λ zwangsläufig größer Null sein, was bedeutet, dass sich Teilchen in diesen Feldern gemäß (90) plötzlich mit einer Ruhemasse m0 und Geschwindigkeiten v kleiner c innerhalb der Lichtkugel bewegen.
Das heißt, dass hier alle im Potentialtopf möglichen Teilchen mit bis hin zu verschwindenden Ruhemassen (Lichtkugel als äußerste Grenze) beschrieben werden können. Durch Δrλϕ ≤ Δrλ ist dabei wegen der dominierenden gravitativen Potentiale immer die maximale integrierte Grenze der potentiellen Teilchenenergien nach

gegeben. Gleichsetzen mit der Grundforderung bestimmter Potentialtopfgrößen gemäß (69) führt dann zu folgender maximalen Ruhemassebeschreibung im definierten Potentialtopf:

Da der Vektor von Δr immer noch eine Funktion des Potentials φŝ+-3 ist, kann man die maximal mögliche Ruhemasse von Teilchen auch über die auf sie einwirkenden Potentialfelder mittels ihrer Ladungen bestimmen. Setzt man voraus, dass die Maximalbeträge der Potentiale IφmaxI in den Potentialtöpfen mit den Ruhemassen m0 korrelieren, zeigt sich nämlich, dass über den Impuls I für die kinetische Energie Ekin eines Elementarteilchens ET
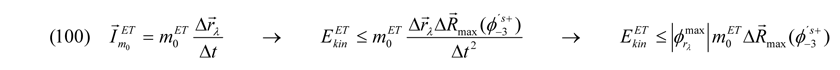
gilt. Offensichtlich ist ebenfalls, dass das Produkt aus der Ruhemasse m0 und des maximalen Raumzeitabstandmaßes Rmax (ohne Abhängigkeit von φŝ+-3!) nichts anderes ist, als das Quadrat eines konstanten Ladungspotentials Q. Damit ist die kinetische Bewegungsenergie Ekin des wechselwirkenden masselosen Teilchens endgültig in die potentielle Energie eines Teilchens mit Ruheenergie bzw. -masse Epot = m0·c2 aus Gleichung (98) inklusive eigenem Ladungspotentialfeld QET umgewandelt worden:
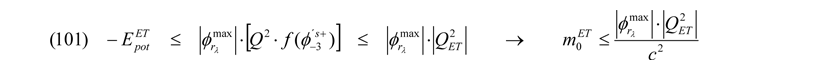
Neben der Erzeugung von Ruhemassen in direkter Abhängigkeit von den Maximalbeträgen der dazugehörigen Feldpotentiale fließen also Ladungen QET ein, welche aufgrund ihrer zweiten Potenz positiv als auch negativ sind und somit mit den Feldpotentialen IφmaxI elektromagnetisch rückkoppeln können. Die in den dementsprechenden Potentialfeldern entstandenen Elementarteilchen sollten sich also durch die Wirkungen ihrer Ladungen mit Unterlichtgeschwindigkeit vorwärts oder auch rückwärts durch die Zeit bewegen, was nichts anderes bedeutet, als dass jedes Elementarteilchen mit exakt der gleichen Ruhemasse in Materie- und Antimaterieform existiert. Gleichartige Ladungen bewegen sich dabei relativ voneinander weg (Abstoßung), entgegen gesetzte Ladungen bewegen sich relativ aufeinander zu (Anziehung). Zur Einsteinschen Ruheenergie E0 = m0·c2 muss somit immer ein mehr oder weniger großer Betrag an Bewegungsenergie Ekin dazukommen. Für gegenüber der Lichtgeschwindigkeit großen und kleinen Geschwindigkeiten gilt in Auswertung der Taylor-Entwicklung nach β:
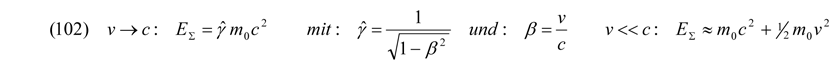
Das heißt, die durch Beschleunigungspotentiale IφmaxI in Rückkopplung mit den Ladungspotentialen QET der Teilchen (elektromagnetische Felder) realisierbaren relativistischen Teilchengeschwindigkeiten können wiederum Wechselwirkungen mit höherenergetischen Feldern hervorrufen und damit sowohl die Ruhemassen erhöhen als auch elektrische Ladungen, Spin, Farben usw. verändern (Bildung neuer Wellen-/Teilchensysteme).
Durch die hier diskutierte Interaktionen der Teilchen mit ihren entsprechenden Feldern entstehen Störungen, welche sich mit Lichtgeschwindigkeit in Form von Wahrscheinlichkeitswellen durch den Raum bewegen, während die Teilchen mit den Wellen assoziiert sind. Die Teilchen (Teilchensystempaare) verursachen also lichtartige (d. h. räumliche) Störungen bei ihrer zeitartigen Bewegung durch den Raum, während sie gleichzeitig mit ihrer Wellenfunktion superponieren. Wenigstens dabei ist leicht einzusehen, dass die lichtschnellen Störungen umso energiereicher sein müssen, desto mehr und stärkere Impulse die Teilchen zu den betreffenden Feldern beitragen. Jeder Impulsübertrag durch das in einem (elektrischen) Feld beschleunigte geladene Teilchen muss mit dem resultierenden lichtschnellen Störungsimpuls (assoziiertes Teilchen-/Wellensystem) des Feldes identisch sein, welcher sich als Quotient des Planckschen Wirkungsquantums ħ und der Wellenlänge der induzierten Störung λSt als inverses Äquivalent (da ħ und c = const.) der Energie einer Welle ergibt:
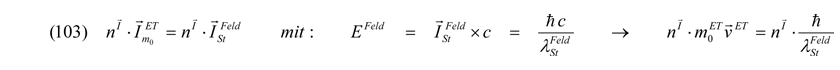
Dieser Zusammenhang stellt nicht anderes als die De-Broglie-Wellenlänge bewegter Teilchen mit Ruhemasse inklusive dem Zusatzterm (Gamma-Faktor) für relativistische Geschwindigkeiten dar. Mit einer allerdings ganz anders gelagerten Ausgangsüberlegung sind wir weiter oben (Gleichung 93) zu genau der gleichen Formulierung gelangt:
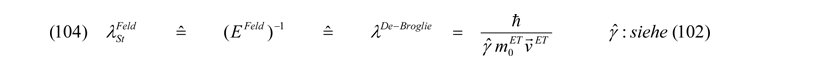
Die Wellenlängen der ausgelösten Störungen in den betreffenden Teilchenfeldern sind somit umgekehrt proportional der Impulse der durch z. B. elektromagnetische Kräfte auf Geschwindigkeit gebrachten Teilchen mit Ruhemasse. Als energiereichste Störung im gegebenen Potential (gleich der Potentialtopfenergie) ergibt sich die Anhilierung gleichartiger entgegengesetzt geladener impulsloser Teilchen, welche sich nur über ihre Ladungen mit einem dann resultierenden Impuls aufeinander zu bewegen (Materie-Antimaterie-Auslöschung). In diesem Fall entspricht das resultierende Produkt aus dem relativistischen Gamma-Faktor und dem Impuls einem theoretischen Nenner von Ruhemasse mal Lichtgeschwindigkeit analog Gleichung (99), was über die Feldenergiegleichung in (103) direkt wieder zu EFeld = m0·c2 führt. Sämtliche Ruhemasse wird damit vollständig in Energie umgewandelt. Besitzen die genannten Materie-/Antimaterieteilchen allerdings einen bestimmten eigenen Anfangsimpuls können neben den energiereichen Photonen (Ɣ-Quanten) auch neue Teilchen entstehen.
Abbildung 14: Potentialgradientenbeträge in den Potentialtöpfen der Kategorien c) und d)
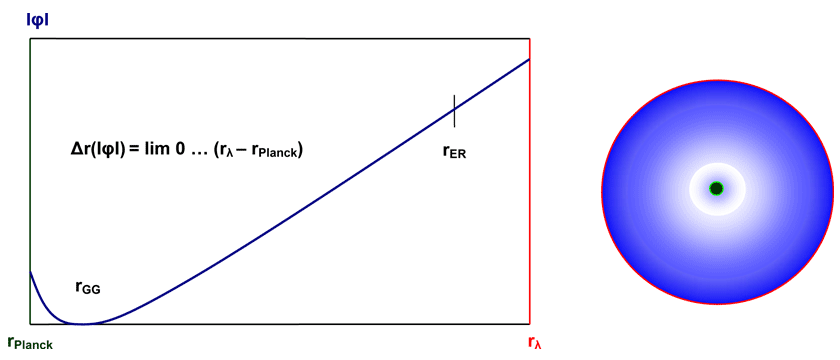
Bezüglich der Raumzeitabstände ergibt sich, wie zu sehen, das gleiche Ergebnis wie in Kategorie b). Das heißt, dass bei den in diesen Potentialenergiespektren interagierenden Teilchen wiederum Masse- und andere Zustände real sein müssen. Ein entscheidender Unterschied ergibt sich jedoch, da jetzt der Entropieradius RER nach Gleichung (84: in Abbildung 13 als rER kenntlich gemacht) ins Spiel kommt. Die unmittelbar vor diesem Radius möglichen relativistischen Impulse erhöhen aber nicht die Energien bis auf unendliche Werte, wie es theoretisch bei gravitativen Potentialen möglich wäre, sondern heben diese aufgrund der inversen Masseabhängigkeit der Formulierung entropischer Potentiale auf einen maximalen Energiewert, welcher dann im weiteren Verlauf ab RER innerhalb der Unbestimmtheitszone konstant bleibt. Ausgehend von Gleichung (82) für das für die Kategorien c) und d) maximale entropische Potential φΣ2,3, ergibt sich für die geleistete Arbeit bzw. aufgenommenen Energie WET(EET) = FEntropie(Rλ) • R(R<Rλ) des Elementarteilchens im Potentialtopf:
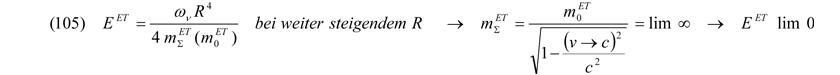
Da die Geschwindigkeit im Potential und damit im relativistischen Falle die Massezunahme von der Arbeit im quantenmechanischen Potential (R<Rλ) abhängt, errechnet sich eine absolute Grenze RER mit der Energie Emax an genau der Stelle, die sich ergibt, wenn man die Bewegungsenergie eines gebundenen Systems mit dem positiven Entropiepotential zu Null annimmt:
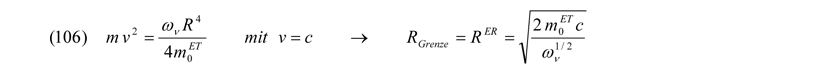
Setzt man diese Grenze RER anstatt von R in die Gleichung (105) ein, erhält man folgende größtmögliche Energie für den entropische Anteil der Arbeit im Potentialtopf Rλ:
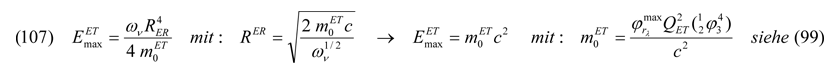
So wie bei den gravitativen Potentialen durch die Definition von Potentialtöpfen gemäß der Heisenbergschen Unschärferelation (siehe 69) im Zusammenhang mit der Superponierungsbedingung über die Planck-Länge (Gleichung 73) unendliche Energiebeträge vermieden werden, geschieht dies genauso in der Kategorien c) und d) mit den dominanten entropischen Potentialen φΣ2,3 über die Einführung der Entropiegrenze RER laut Gleichung (84). Die Maximalenergien sind dabei, egal ob diese durch gravitative oder entropische dominierte Potentialtöpfe induziert worden sind, in jedem Falle nicht größer als das Einsteinsche Energie-Masse-Äquivalent, was die Gleichungen (98) und (107) aussagen.
In den Potentialtöpfen der Kategorien b), c) und d) werden also mit abnehmender Tendenz und Energie Teilchen mit Ruhemasse generiert. Gemäß Gleichungen (93) und (101) tragen dabei alle Teilchen eine konstante Ladungsgröße, welche sich aber über die Abhängigkeiten in den auftretenden Potentialen φ1 bis φ4 individualisiert aufspalten und damit Informationen über Spin, Materie oder Antimaterie, elektrische Ladung, Magnetismus, Farb- und Schwache Ladung und andere Quantenzahlen tragen sollten.
Durch Wechselwirkungen der Teilchen mit den stationären Schwingungszuständen in den Potentialtöpfen treten wie beschrieben interferenzfähige lichtartige Störungen auf, während die Teilchen im gleichen Augenblick mit den Störungswellen solange assoziiert sind, solange nun wiederum von außen keine Störung auf die Teilchenwelle einwirkt. Über die impulsinduzierten resultierenden Energien können alle Photonen emittierende Störungen als völlig identisch mit den Photonen der Kategorie e) angesehen werden. Das bedeutet im Umkehrschluss ebenso, dass genau aufeinander entgegengesetzt gerichtete Impulse (= Energien) der Photonen aus Kategorie e) vollständig in die entsprechenden mit Ruhemasse behafteten Teilchen und Antiteilchen der Kategorien b) bis d) umgewandelt werden können.
Abbildung 15: Potentialgradientenbeträge in den Potentialtöpfen der Kategorie e)
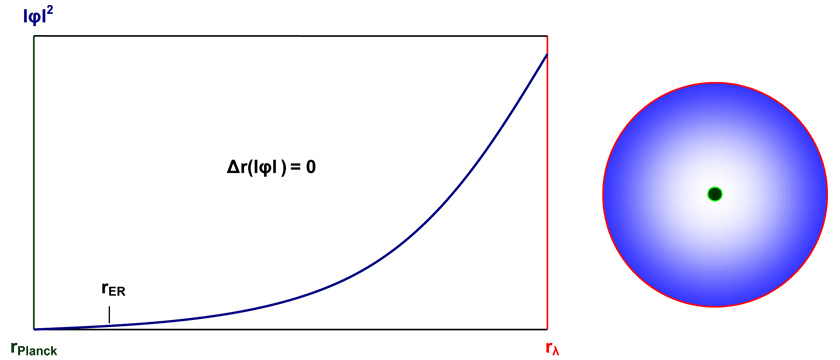
Wie in Kategorie a) kommt man auch in der Kategorie e) zu dem Schluss, dass wegen der symmetrischen Verteilung jetzt ausschließlich entropischer (positiver) Potentiale das kartesische Raumabstandsmaß Null ist und es sich damit um ruhemasselose Systeme handeln muss. Dabei zeigt sich über die energetische Betrachtung der Potentiale φ1 und φ4 aus Gleichung (82), dass nun entgegen der Heisenbergschen Unschärfedeutung die maximalen Energiebeträge nicht weiter fallen, sondern plötzlich steigen, weil:
![]()
Die Berechnung der entropischen Energie der Potentiale φ1 und φ4 über die gesamte Potentialtopflänge Rλ ist deswegen legitim, weil bei den besagten entropischen Potentialen ja nur jeweils einzeln zu betrachtende Planck-Längen aufkumuliert werden. In den viel größeren entropischen Potentialen φ2 und φ3 hingegen sind Abstände zwischen den virtuellen Teilchen über die Planck-Länge hinaus Berechnungsgrundlage, sodass dann die integrierten Energien über die Berücksichtigung des Entropieradius RER immer auf ħ/Rλc begrenzt bleiben müssen.
Die auch hier zu interpretierenden ausgelösten Störungen durch ruhemasselose Teilchen haben also über den lichtschnellen Impuls interferenzfähige Wellen mit Energien zur Folge, welche alle Energien der Kategorien a) bis d) abdecken. Das heißt nichts anderes, dass die Welle-/Teilchensysteme der Kategorie e) bei Energien von ca. 10-34 eV bis 505 GeV nichts anderes sind, als die in den Kategorien b), c) und d) emittierten Photonen mit Spin 1. Das bedeutet aber im Umkehrschluss genauso, dass Photonen der Kategorie e) mit passend aufeinander gerichteten Impulsen zu mit Wellen assoziierten Teilchen der Kategorien b), c) und d) umgewandelt werden können.
In diesem Kapitel sollte im Besonderen aufgezeigt werden, dass die Allgemeine und die Spezielle Relativitätstheorie (RT) ausschlaggebend für das Verständnis sowohl des Welle-Teilchen-Dualismus als auch für die Generierung von Elementarteilchen sein dürften. Für die Entstehung der Ruhemassen wiederum ist das Vorhandensein entropischer Potentiale entscheidend, welche die Raumzeit und damit auch die Felder in den Potentialtöpfen ins Negative und damit asymmetrisch krümmen. Treten nur gravitative bzw. nur entropische Potentiale in den „Heisenbergschen Unschärfetöpfen“ einzeln auf, entstehen ruhemasselose Bosonen. Sind beide Potentiale gemeinsam vertreten, können sich durch die Berücksichtigung der RT Bosonen und Fermionen mit Ruhemasse entwickeln. Jeder Potentialtopf hat dabei seine individuelle Raumzeitkrümmung, das heißt, dass an sich ruhemasselose Teilchen ihre charakteristischen trägen Massen erhalten, je nachdem, in welchen asymmetrischen Feldern diese zu beobachten sind. Grundlage für sämtliche Betrachtungen ist die Einvernehmlichkeit der Gravitation (zusammen mit den entropischen Potentialen) mit quantenphysikalischen Aspekten. Wie noch in den folgenden Kapiteln zu sehen, sind die Kräfte der Quantengravitation sowie -entropie innerhalb ihrer definierten Potentiale und Grenzen im Zusammenhang mit der RT, der Sommerfeld-Ableitung und der Heisenbergschen Unbestimmtheitsrelation die Initiatoren sowohl für die Entstehung der Elektromagnetischen, der Schwachen und der Starken Wechselwirkung als auch der makroskopischen Gravitationskraft. >>>zurück zur Auswahl<<<
>>> zum nächsten Kapitel (Massen, Ladungen und Energien von Elementarteilchen) >>>
